メモ帳

PLDA (Probabilistic Linear Discriminant Analysis) の基礎と応用 2025年12月22日更新

話者認証や音声バイオメトリクスで広く用いられている PLDA の原理と、実務で押さえておきたい実装ポイントを整理します。

PLDA 話者認証 音声セキュリティ

PLDA とは何か

PLDA (Probabilistic Linear Discriminant Analysis) は、同じ答えのデータごとにグループを作り、確率的にどのグループに属するかで答えを判別する手法です。話者認証では i-vector や x-vector の埋め込みを コサイン類似度を使って判別する手法が多く用いられていますが、より統計的に強力なPLDA で判別する手法も取られます。

ベクトルAとベクトルBのコサイン類似度を三次元空間で可視化した図

図1. ベクトル間の角度 θ が小さいほどコサイン類似度が高くなる

PLDA はベクトル空間内で同一話者の埋め込みが共通の確率分布に従うと仮定し、クラスごとの広がりや重なり具合を統計的にモデリングします。下図は、2 次元上で発話ごとの特徴点が話者ごとにクラスタを形成しているイメージです。

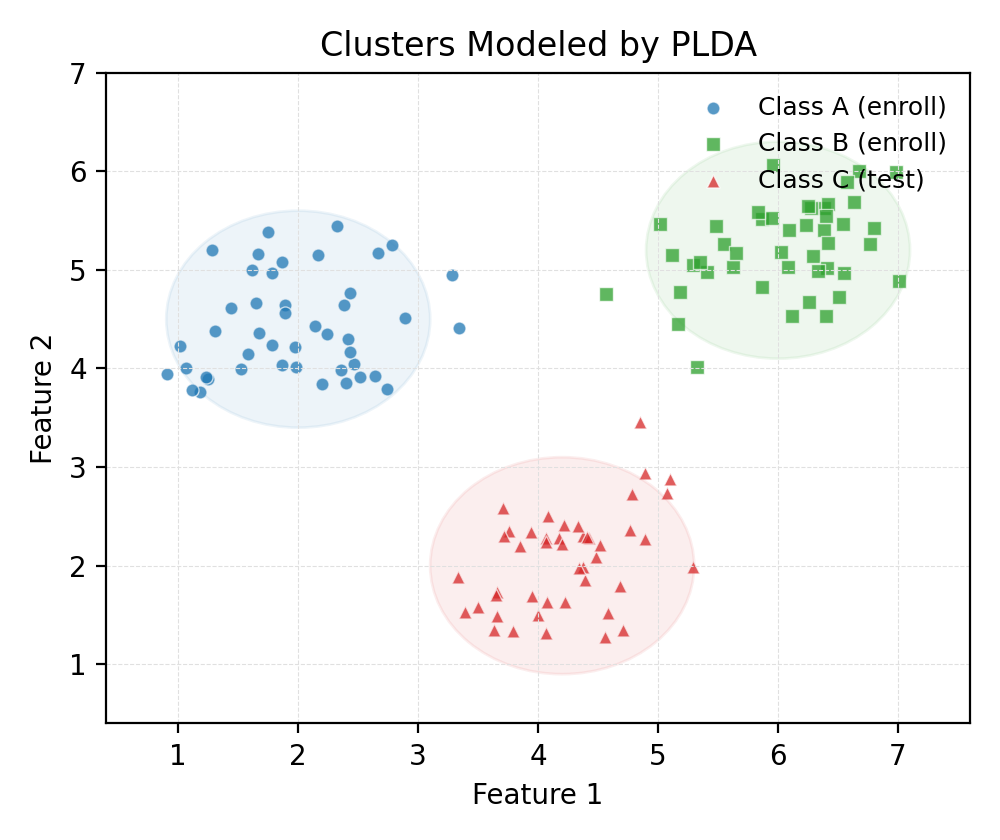
PLDA が想定する話者ごとのクラスタ構造イメージ

図2. 同じ話者に属する埋め込みは同心的な分布を形成し、PLDA がクラス間の境界を推定する

  • 各発話が話者固有ベクトル + セッション雑音の線形結合として生成されると仮定
  • 話者固有ベクトルと雑音は多変量ガウス分布に従うと想定
  • ベイズ推定により、話者間類似度 (log-likelihood ratio) を計算可能

前提となるパイプライン

段階 処理内容 出力
特徴抽出 MFCC / FBANK / Spectrogram などを計算 フレーム系列 (T × D)
埋め込み抽出 i-vector や x-vector モデルで固定長ベクトル化 ベクトル z ∈ ℝⁿ
次元圧縮・正規化 LDA, PCA, Whitening などで分布整形 正規化済の埋め込み
PLDA 学習 EM アルゴリズムで各トレーニング話者のクラス分布を推定 Σ_between, Σ_within 等のパラメータ
スコアリング 検証発話と登録発話の尤度比を算出 LLR スコア

PLDA は独立したモジュールとして設計できるため、既存の埋め込みモデルを差し替えても再利用しやすいメリットがあります。

確率モデルの定式化

生成モデル

各発話埋め込み z は、話者固有の隠れ変数 y と、セッション固有の雑音 ε から生成されると仮定します。


y ~ 𝒩(0, I)
ε ~ 𝒩(0, Σ_w)
z = μ + Fy + ε
  • μ: グローバル平均
  • F: 話者因子行列 (eigenvoice matrix)
  • Σ_w: セッション内分散

尤度比スコア

2つの埋め込み z_1, z_2 が同一話者か否かの仮説検定を行う場合、以下の尤度比が用いられます。


score = log p(z_1, z_2 | H_same) - log p(z_1 | H_diff) - log p(z_2 | H_diff)

ガウス積分を解析的に解ける点が PLDA の大きな利点です。実装では共分散行列の逆行列計算や Cholesky 分解を用いることが多いです。

学習手順 (EM アルゴリズム)

  1. E-step: 観測データと現状のパラメータから y の事後分布を推定
  2. M-step: 推定された y を用いて行列 F と共分散 Σ_w を更新
  3. 収束判定: 対数尤度の増加量が閾値以下になったら終了

初期化には PCA やランダム初期値が用いられます。実務では 5〜10 回程度の EM で収束することが多いですが、特異行列を避けるために正則化 (diagonal loading) を入れると安定します。

ハイパーパラメータ設計

  • 埋め込み次元: x-vector の場合は 256〜512 次元が一般的。PLDA 前に 150〜200 次元に圧縮することが多い。
  • 話者数と発話数: 1 話者あたり最低でも 10 発話程度が望ましい。ドメイン適合を重視する。
  • 正則化: Σ_w に対して λI を加えるなど、数値安定性を確保。
  • ドメイン適応: PLDA はテスト環境へのドメイン適応が重要。特定環境で追加学習を行うことで EER が大幅に改善する。

Python 実装例 (Kaldi 風)

import numpy as np
from numpy.linalg import cholesky, inv

class PLDA:
    def __init__(self, dim, y_dim):
        self.mean = np.zeros(dim)
        self.F = np.random.randn(dim, y_dim) * 0.1
        self.Sigma_w = np.eye(dim)

    def e_step(self, X):
        # X: (n_samples, dim)
        centered = X - self.mean
        Sigma_y = np.eye(self.F.shape[1]) + self.F.T @ inv(self.Sigma_w) @ self.F
        Sigma_y_inv = inv(Sigma_y)
        posterior_mean = Sigma_y_inv @ self.F.T @ inv(self.Sigma_w) @ centered.T
        return posterior_mean.T, Sigma_y_inv

    def m_step(self, X, post_mean, post_cov):
        centered = X - self.mean
        n = X.shape[0]
        Ey = post_mean
        Eyy = post_cov + Ey.T @ Ey / n
        self.F = centered.T @ Ey @ inv(Eyy)
        residual = centered - Ey @ self.F.T
        self.Sigma_w = (residual.T @ residual) / n

    def fit(self, X, n_iters=10):
        for _ in range(n_iters):
            post_mean, post_cov = self.e_step(X)
            self.m_step(X, post_mean, post_cov)

    def score(self, enrollment, test):
        # enrollment/test: (dim,)
        # ここでは簡略化した2クラス尤度比
        return -np.dot(enrollment - test, inv(self.Sigma_w) @ (enrollment - test))

実際の Kaldi や pyannote.audio ではより高度なバックエンドを採用していますが、仕組みの理解には上記のようなミニマル実装が役立ちます。

評価指標と実務での着眼点

  • EER (Equal Error Rate): 認証システムの総合性能を確認するための指標。PLDA 導入前後の比較で改善を測定。
  • DET カーブ: 操作点毎の false accept / false reject のバランスを視覚化。
  • スコア校正: PLDA スコアはシンプルなロジット変換でキャリブレーション可能。後段の閾値設定が安定。
  • 攻撃耐性: VC 系攻撃のような合成音声に対しては別途 CM (countermeasure) を組み合わせるのが必須。

まとめ

PLDA はクラシックな手法ながら、最新の深層学習ベース埋め込みとも相性が良く、話者認証のバックエンドとしていまだに現役です。ドメイン適応やスコア校正とセットで運用することで、堅牢かつ高精度な認証を実現できます。

関連リンク